« Lorsque les concepts abstraits et les applications sont maîtrisés et adaptés au public, les mathématiques deviennent une grande source d’émerveillement »

La spécialité de Julien Marché ? Les nœuds ! Ce professeur à Sorbonne Université, rattaché au département de mathématiques de l’ENS-PSL depuis septembre 2024, étudie la topologie dite de basse dimension, qui s’intéresse à la forme et la géométrie des objets en petite dimension, c’est-à-dire jusqu’à quatre. La topologie inclut la célèbre théorie des nœuds, un domaine des mathématiques aujourd’hui particulièrement actif. «Un nœud est simplement une façon d’emmêler une corde : en général on préfère refermer cette corde sur elle-même comme dans la table de nœud en exemple ci-dessous », explique-t-il. Mais comme le soulignait la mathématicienne suisse, Éva Bayer, « bien que simple à définir, un nœud peut être un objet très compliqué (1)».

Les nœuds, concept clé dans les mathématiques
« Un but – malheureusement vain – serait d’établir un catalogue de tous les nœuds dans lequel chacun apparaîtrait à un endroit logique et toutes ses propriétés seraient référencées », précise Julien Marché. N’en déplaise aux mathématiciens qui, depuis le XIXe siècle, étudient les nœuds pour comprendre leur géométrie, les comparer et les classer.

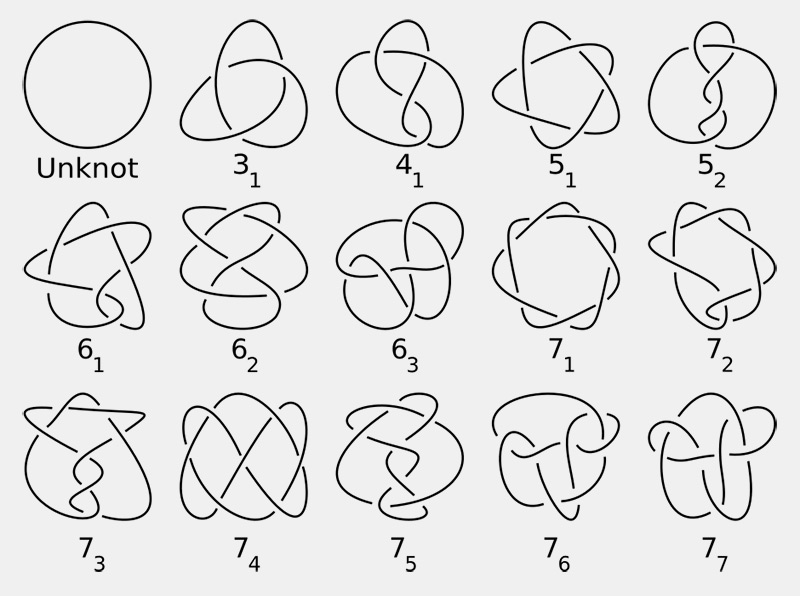
Table des nœuds premiers réalisables avec au plus 7 croisements.
Le produit de deux nœuds s'obtient en coupant chaque nœud et en recollant les extrémités libres. Le cercle joue le rôle d'unité pour ce produit. Comme les nombres premiers, qui ne peuvent être divisés que par eux-mêmes et par 1, les nœuds premiers sont ceux qu'on ne peut décomposer en produit de nœuds plus simples. On a montré que tout nœud se décompose de façon unique, à l'ordre près, en produit de nœuds premiers. La classification des nœuds premiers est aujourd'hui connue jusqu'à 20 croisements : il en existe 1 847 319 428. 
Source : The enumeration and classification of prime 20–crossing knots, Morwen B. Thistlethwaite

 « La théorie des nœuds est attirante, car elle parle d’objets concrets qu’on peut même collectionner dans son bureau »

Or, il se trouve que les nœuds sont loin d’être un objet isolé au sein des mathématiques. Ils permettent de représenter toutes les « variétés de dimension 3 », à savoir toutes les formes possibles d’un espace à trois dimensions. 
Ces espaces interviennent aussi bien dans de nombreuses questions mathématiques abstraites, lieux des solutions d’équations, que concrètes, c’est-à-dire dans la forme et les propriétés d’un espace physique. Les nœuds seraient-ils – presque – partout dans les mathématiques, mais aussi ailleurs ? « La théorie des nœuds est attirante, car elle parle d’objets concrets qu’on peut même collectionner dans son bureau », estime Julien Marché. « Pour autant, ces objets, une fois formalisés, prennent leur place dans le grand bestiaire des mathématiques comme les polyèdres (2), les corps de nombres ou les graphes (3), et interagissent avec eux d’une manière subtile », ajoute-t-il. « Elle n’a pas vraiment d’application directe dans la vie de tous les jours, même si certains chercheurs essaient d’en trouver par exemple dans l’enchevêtrement de l’ADN ou dans la structure spatiale d’une longue chaîne de protéines ».

Pour le scientifique, la théorie des nœuds est avant tout « un outil » pour se représenter des espaces complexes. Dans un exposé grand public, donné lors de Timeworld, un congrès mondial autour de la construction, il imagine chaque nœud représenter le chambranle d’une porte permettant de basculer dans un autre monde.

Des grandes questions encore irrésolues
Julien Marché se place ainsi « naturellement » dans une longue tradition de recherche fondamentale, non dédiée aux applications. « Si l’hypothèse de Riemann était démontrée ( l’un des problèmes mématiques ouverts les plus célèbres ), cela ne changerait rien à la vie de personne, pour autant cela me semblerait une conquête inestimable, améliorant significativement notre compréhension de la répartition des nombres premiers. », relativise-t-il. 
Comme dans tout domaine de recherche, celui de Julien Marché est jalonné de grandes questions encore irrésolues : «  l’une des plus belles est la conjecture de Poincaré en dimension 4 », considère-t-il. « Soit, en termes techniques, est-ce que toute variété compacte simplement connexe de dimension 4 est difféomorphe à la sphère ? » Cette réponse, positive, à cette question en dimension 3 a mobilisé les chercheurs pendant pas moins d’une centaine d’années, « permettant au mathématicien russe Perelman au début des années 2000 d’achever le programme de géométrisation de Thurston qui structure considérablement notre compréhension de la topologie à 3 dimensions. », explique le scientifique. « La version en dimension 4 promet d’être encore plus difficile, alors que curieusement, la version en dimension 5 et plus a été démontrée dans les années 1960 ! », poursuit-il. « C’est assez ironique car le champ d’application naturel de ces questions est de déterminer la structure topologique de notre espace-temps qui a précisément 4 dimensions. » 

L’esprit curieux

Des recherches fondamentales donc, mais aussi interdisciplinaires, à l’interface des mathématiques et de la physique, au croisement de la théorie des nœuds et de la théorie quantique des champs. « Cette dernière est la base du “modèle standard”, rendant compte de notre compréhension actuelle de l’infiniment petit », indique le chercheur. « Le mathématicien-physicien Edward Witten a découvert en 1989 comment une version “topologique” de la théorie quantique des champs,  c’est-à-dire insensible aux déformations de l’espace, retrouvait des “invariants” de nœuds qu’on venait de découvrir – le polynôme de Jones – et dont le sens géométrique nous échappait », explique-t-il.  Pour Julien Marché, cette interaction est une grande source d’inspiration : « et je constate qu’elle a le même effet sur mes étudiants d’aujourd’hui », observe-t-il. « Je crois donc fortement à l’interdisciplinarité mais je ne suis pas sûr de savoir bien la valoriser, ne vient-elle pas naturellement à tout esprit curieux ? »

Un esprit curieux que Julien Marché développe depuis tout petit, « très tôt passionné » par les thèmes scientifiques, tels que l’astronomie ou l’informatique. « J’ai probablement été influencé par mon père, ingénieur et bricoleur », se souvient-il. À partir de la classe de première, c’est la recherche qui devient « une évidence » pour l’adolescent. « Bien que très scolaire, je ne m’intéressais que vaguement aux cours, jusqu’à ce que ceux-ci abordent des mathématiques un peu avancées. »

 « l’approche mathématique permet à la fois de calculer des solutions et de prouver qu’il n’y en a pas d’autres. »

Julien Marché se souvient particulièrement de sa découverte des équations différentielles, « indispensables pour comprendre les équations du mouvement, ou le fonctionnement des réseaux électriques », indique-t-il. « J’ai découvert que l’approche mathématique permettait à la fois de calculer des solutions et de prouver qu’il n’y en avait pas d’autres. »  Le début d’une « révélation », qui ne fera que se confirmer et s’intensifier dans les années qui suivent.  « Ce qui m’a plu dans les maths ? À la fois l’accès à un savoir qui me semblait à la fois mystérieux et infini – et c’est toujours le cas – une certaine efficacité dans l’application de ce savoir, et enfin une méthode exigeante, la démonstration, pour ne pas en douter. »

Après son bac, Julien Marché poursuit par une classe préparatoire scientifique dans le Sud-Ouest familial, à Toulouse. Il intègre ensuite le département de mathématiques et applications de l’ENS-PSL. « Un cadre exceptionnel pour mes études, essentiellement par le biais des interactions avec les autres étudiants, tous d’horizons différents, mais tous passionnés par les maths », indique-t-il. « La possibilité de passer tout mon temps avec eux a été probablement la meilleure formation que j’ai pu avoir, d’autant plus qu’elle était encadrée par des enseignants-chercheurs plus que compétents. »

Julien Marché poursuit par une thèse à l’Université Paris Cité, qu’il obtient en 2004. Le scientifique devient ensuite successivement maître de conférences et professeur à Sorbonne Université. Entre ces deux postes, il est détaché trois ans à l'École Polytechnique. Actuellement professeur à Sorbonne Université, il enseigne depuis septembre 2024 aux étudiantes et étudiants de 1re et 2e année à l’ENS-PSL qui suivent le cursus de mathématiques.Il encadre en ce moment des groupes de travail sur des sujets mathématiques divers : les graphes expanseurs, ou comment fabriquer des graphes arbitrairement grands et extrêmement bien connectés, et le problème des congruences-ciseaux aussi appelé troisième problème de Hilbert et qui s’énonce ainsi : “à quelle condition un polyèdre peut-il être découpé et recombiné pour en fabriquer un autre ?”. « J’aime ces sujets car, si la question peut être comprise par tout le monde, la solution fait intervenir une grande quantité de maths, parfois récente, souvent abstraite, mais qui finit toujours par trouver du sens. »

Un conseil d’ailleurs pour toute personne souhaitant poursuivre une carrière dans la recherche en mathématiques ? « Ne donner aucune limite à sa curiosité, prendre confiance en soi, tirer profit de toute expérience et… ne pas trop écouter les conseils », sourit-il.

La vulgarisation scientifique : un exercice difficile

Aujourd’hui c’est en tant qu’enseignant que Julien Marché repense à celles et ceux dont il occupe aujourd’hui la place : « Tout au long de ma formation, à l’ENS et ailleurs, j’ai rencontré des professeurs, puis des chercheurs, qui m’ont énormément appris », témoigne-t-il. « Il est difficile d’en distinguer certains, je me tiendrais à souligner à quel point l’art d’enseigner les maths est subtil, sublimé par le tableau noir et la craie », poursuit-il. « L’enchaînement des définitions de concepts abstraits, d’applications et d’exercices quand il est bien maîtrisé et adapté au public, est une grande source d’émerveillement. » Amateur du style « austère mais limpide » de son directeur de thèse Pierre Vogel, Julien Marché cite également Étienne Ghys, mathématicien renommé et grand vulgarisateur, « capable de rendre tout sujet passionnant. »

 « rien ou presque ne nous prépare à la vulgarisation scientifique en tant que chercheur, et cela repose sur des qualités différentes de celles qui nous ont généralement permis de faire carrière. »

Intéressé depuis toujours par la vulgarisation scientifique autant comme public que comme vulgarisateur, Julien Marché estime cependant l’exercice peu évident : « rien ou presque ne nous y prépare en tant que chercheur, et cela repose sur des qualités différentes de celles qui nous ont généralement permis de faire carrière. » Il y a par exemple la crainte de perdre ou de décevoir « notre public non averti ou nos collègues qui nous jugent en retour ». Mais qu’à ne cela tienne, le chercheur s’est lancé. Et s’il a pu affronter quelques difficultés, Julien Marché ne regrette pas l’expérience : « mes deux dernières tentatives m’ont demandé beaucoup de travail, rapporté très peu de retours, mais procuré malgré tout une certaine satisfaction », confie-t-il.
Lors de la dernière, qui consistait à donner un exposé grand public, à Timeworld (mentionné précédemment), Julien Marché a tenté d’expliquer la notion de revêtement double le long d’un entrelacs à l’aide de portes en bois, qu’il avait lui-même bricolées. « J’ai essayé d’y mettre un peu de poésie sans sacrifier à la rigueur scientifique », explique-t-il. Le chercheur songe désormais à consacrer plus de temps à la vulgarisation scientifique, en espérant toucher un public plus nombreux les prochaines fois, « même si je n’ai pas l’âme - ni peut-être le talent - d’un youtubeur ! », conclut-il.  
 

(1)    Discours d’Éva Bayer lors de la 71e conférence de l’Université de tous les savoirs donnée le 19 juin 2000 à l’ENS-PSL.
(2)    Polyèdre : un polyèdre est une forme géométrique à trois dimensions (un solide géométrique) ayant des faces planes polygonales qui se rencontrent selon des segments de droite qu'on appelle arêtes. Une pyramide est par exemple un polyèdre.
(3)    Graphe : on appelle graphe la donnée d'un ensemble de points appelés sommets et d'un ensemble de lignes appelées arêtes qui relient certains sommets entre eux.